PROGRAMACIÓN FUNCIONAL

¿Se puede liberar la programación del estilo von Neumann? (John Backus)

“Lo que fue nuevo y esencial para toda la matemática fue la concepción enteramente general de función” (Dedekind)

---

El Paradigma Funcional
El paradigma funcional de programación se basa en utilizar un solo concepto (o primitiva conceptual): la función, en el sentido matemático del término. Nació como reacción al paradigma imperativo. John Backus ha sido uno de los máximos impulsores de la semántica funcional de programación, criticando el concepto de variables y el de sentencias de asignación, afirmando que son la raíz de muchos males y una “maldición” transmitida por el modelo von Neumann [Backus, 1978].


Características del paradigma funcional

• Uniformidad.
  Todo es una función. En los lenguajes funcionales (también llamados aplicativos), todas las construcciones son funciones. A una función se le “aplican” datos de entrada (argumentos de la función) para obtener un resultado (calculado por la función), que depende únicamente de dichos argumentos. No hay efecto laterales: una función no tiene más efecto que la producción del resultado a partir de los argumentos.
  
  
• Transparencia referencial.
  En general, la transparencia referencial se refiere a que, en un programa de tipo funcional, la semántica de una expresión es siempre la misma, independientemente del lugar que ocupe dentro del programa. Es decir, la evaluación de la expresión siempre produce el mismo resultado. Esto no ocurre con la programación imperativa, pues las sentencias de asignación de valores a variables, hace que una misma expresión no signifique lo mismo en diferentes puntos del programa.
  
  Las ventajas de la transparencia referencial son:
  
  
  1. Las modificaciones que se hacen en una función no afectan al resto de las funciones.
     
     
  2. Facilitan la verificación de los programas, es decir, la demostración matemática de que cumplen la especificación.
  
  
• Especificación.
  Los lenguajes funcionales permiten especificar los procesos o transformaciones que hay que realizar con los datos sin necesidad de realizar referencias implementadoras. Al diseñar un programa se hace abstracción del qué hacer antes de especificar el cómo debe hacerse. Las funciones son los vehículos de este primer tipo de abstracción.
  
  
• Jerarquía.
  El argumento de una función puede ser otra función. De esta forma se construyen funciones de orden superior. Un programa es también una función que está en lo más alto de la jerarquía de las funciones utilizadas.
  
  
• Recursión.
  Las funciones pueden llamarse a sí mismas, lo que simplifica notablemente la programación.
  
  
• Polimorfismo.
  Es una característica soportada por muchos lenguajes funcionales. Una función polimórfica acepta parámetros de diferentes tipos de datos. Esta flexibilidad permite construir funciones genéricas o de alto nivel, sin necesidad de crear diferentes versiones de funciones para cada uno de los tipos de datos.

Limitaciones del paradigma funcional

La aplicación exclusiva del paradigma funcional conduce a graves dificultades expresivas:

• El énfasis se pone en las funciones, es decir, en los procesos de los datos, y en el proceso de descomposición funcional. Los datos tienen un papel secundario y emergen durante estos procesos.
  
  
• No es posible realizar actualizaciones in situ de las estructuras de datos.
  Las estructuras de datos hay que construirlas totalmente cada vez, aunque sólo se haya modificado un elemento. Un intento de evitar esto son las llamadas “estructuras de datos funcionales” consideradas como objetos actualizables, accesibles por las funciones del lenguaje [Milewski, 1990].
  
  
• Pobreza de estructuras de datos.
  La mayoría de los lenguajes funcionales usan la lista como la única o la más importante estructura de datos.
  
  
• No hay sentencia de asignación ni variables globales.
  Aunque ambas se pueden emular mediante parámetros de función, la verdad es que ello supone una grave limitación de expresión. Es por ello que algunos lenguajes funcionales como Lisp las incorporan.
  
  
• Ausencia de estados internos.
  Esto es consecuencia de la falta de efectos laterales. El comportamiento de una función es siempre el mismo con los mismos argumentos de entrada. Esto implica dificultad para modelar el mundo real, en el que el comportamiento varía dependiendo del estado interno de los objetos.

Especificación en MENTAL
Definición de función

Una función f es una expresión dependiente de uno o varios parámetros que, al ser evaluada con los mismos argumentos produce siempre el mismo resultado.

• Todos los parámetros son de entrada. Los parámetros son expresiones.
  
  
• Hay una única salida, que es el resultado de la función, que es una expresión. Esta expresión de salida puede ser de cualquier tipo y tan compleja como se quiera.

Formas de especificar y evaluar funciones

Existen muchas formas de especificar y evaluar funciones: de forma directa (sin nombre), con nombre, con y sin parámetros formales, con o sin evaluación diferida, con sustituciones absolutas o relativas, con evaluación parcial o total, etc.

• Mediante una expresión directa (sin nombre) con argumentos relativos:
  
  (x+y+3)/(y=1) // ev. x+4

(x+y+3)/{x=1 y=2} // ev. 6
  
  
• Mediante una expresión de sustitución, sin parámetros formales, con los argumentos especificados de forma absoluta (en línea):
  
  (z = (x+y+3)°) // ev. (z = x+y+3)

(y = 1)

z // ev. x+4 (evaluación parcial)

(x=1 y=2)

z // ev. 6 (evaluación total)
  
  
• Mediante una expresión de sustitución, sin parámetros formales y con sustitución relativa:
  
  ( z = (x+y+3)° )

z/(y = 1) // ev. x+4 (evaluación parcial)

z/((x = 1) (y = 2)) // ev. 6 (evaluación total)
  
  
• Mediante una expresión de sustitución con parámetros formales, de forma mixfija en general:
  
  
  1. ⟨( f(x y) = (x+y x*y) )⟩
f(3 4) // ev. (7 12)
     
     
  2. ⟨( (a x b y) = (a ← x<y →’ b) )⟩
(a 3 b 4) // ev. a
(a 4 b 3) // ev. b
  
  
• Mediante una expresión de sustitución, con o sin parámetros formales, que produce un resultado consecuencia de un proceso:
  
  
  1. ( z = (( (i = 1) (i = i*2)★n ¡i )!)° )
z/(n = 4) // ev. 16
     
     
  2. ⟨( z(n) = ((i = 1) (i = i*2)★n ¡i)! )⟩
z(4) // ev. 16
  
  
• Mediante una expresión sin nombre, que denota un proceso, sin parámetros formales y con sustitución relativa:
  
  ( ((i = 1) (i = i*2)★n ¡i)°/(n=4) )! // ev. 16

Ejemplos de funciones con parámetros

En los ejemplos siguientes, por su mayor claridad, vamos a utilizar expresiones genéricas parametrizadas para definir funciones.

1. Serie de Fibonacci.
   Produce una secuencia con los n primeros números de la serie de Fibonacci.
   
   ⟨( fibo(n) = ( (n=1 → ¡1 )
(n=2 → ¡(1 1))
(s = fibo(n−1))
¡(s↓ (s\(s#) + s\(s#−1)))
)!
)⟩

fibo(1) // ev. 1
fibo(2) // ev. (1 1)
fibo(3) // ev. (1 1 2)
fibo(8) // ev. (1 1 2 3 5 8 13 21)
   
   
2. Conversión de una secuencia x de dígitos binarios a un número decimal.
   El procedimiento consiste en multiplicar el primer dígito por 2 y sumarle el segundo, multiplicar el resultado por 2 y sumarle el tercero, etc., hasta llegar a sumar el último. Por ejemplo, 1011 = ((1*2 + 0)*2 + 1)*2 + 1.
   
   ⟨( bindec(x) = ( (r = 0)
[(r = (r*2 + x\[1…x#]))]
¡r )! )⟩

bindec(1011) // ev. 11
   
   
3. Conversión de un número entero positivo n en una secuencia de dígitos binarios.
   El procedimiento consiste en dividir el número n entre 2, el cociente se vuelve a dividir entre 2, etc. hasta que el cociente sea 1. Entonces se toma el último cociente y todos los restos en orden inverso. Ejemplo para el número 19:
   
   

   Oper.	Cociente	Resto	Resultado
   19÷2	9	1←	10011
   9÷2	4	1←
   4÷2	2	0←
   2÷2	1←	0←

   
   ⟨( decbin(n) = ( (s = ()) // secuencia resultado inicial

(m = n)

( (c = m÷2)) // cociente

(c=1 → ¡(c s↓))

(r = resto(m 2)) // resto

// incluir resto al comienzo de la secuencia

(s = (r s↓))

(m = c) )★ )! )⟩

decbin(19) // ev. (1 0 0 1 1)
   
   
4. Función que devuelve ”S” si n es primo y ”N” en caso contrario.
   
   ⟨( primo(n) = ( n≤3 → ¡"S")
((resto(n 2) = 0) → ¡"N")
[ (i = [(3 … nv2)])
((resto(n i) = 0) → ¡"N") ]
¡"S" )! )⟩
   
   Siendo
   
   ⟨( resto(n1 n2) = n1 – (n1÷n2)*n2 )⟩
   
   el resto de la división entre dos números enteros. La expresión nv2 es la parte entera de √n.

Funciones recursivas

Son funciones que se llaman a sí mismas. El uso de la recursividad simplifica notablemente la definición de funciones.

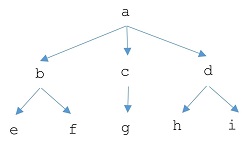
Un ejemplo representativo es el de los recorridos en amplitud y profundidad de un árbol. Si tenemos el árbol


es decir,

( árbol = ( (a b) (a c) (a d)
(b e) (b f) (c g) (d h) (d i) ) )

o bien, usando la distribución,

( árbol = ( [(a [b c d])]
[(b [e f])] (c g) [(d [h i])] ) )

en donde (x y) representa la rama del árbol que va del nodo x al nodo y.

Recorrido del árbol en amplitud (nodo es el nodo raíz):

⟨( amplitud(árbol nodo) = (
(s = (⟨ (x ← (nodo x)∈árbol ⟩) // secuencia de nodos hijos
(¡( nodo ) ← s=() →'
¡( nodo s↓ [amplitud(árbol [s↓])↓] )
)! )⟩

amplitud(árbol a) // ev. (a b c d e f g h i)
amplitud(árbol b) // ev. (b e f)
amplitud(árbol e) // ev. ( e )

Recorrido del árbol en profundidad (nodo es el nodo raíz):

⟨( profundidad(árbol nodo) = (
(s = (⟨ (x ← (nodo x)∈árbol ⟩) // secuencia de nodos hijos
(¡( nodo ) ← s=() →'
¡( nodo s\1 [profundidad(árbol ([s ∪’ s\1])↓] )
)! )⟩

profundidad(árbol a) // ev. (a b e f c g d h i)
profundidad(árbol b) // ev. (b e f)
profundidad(árbol e) // ev. ( e )


Tablas

Una tabla es un caso particular de función en la que hay una correspondencia explícita y directa entre cada argumento y su resultado.

Ejemplos:

1. Función y definida sobre un argumento x:
   
   

   x	y
   1	2
   2	7
   3	5
   resto	8

   
   ⟨( y(x) = (2 ← (x=1) →'
(7 ← (x=2) →'
(5 ← (x=3) →’ 8))) )⟩
y(2) // ev. 7
y(4) // ev. 8
y("abc") // ev. 8
   
   
2. Función z de dos argumentos (x, y) en donde α indica “cualquier expresión”:
   
   

   x	y	z
   x	y	z
   0	0	a
   0	1	b
   α	0	c
   1	α	d

   
   ⟨( z(x y) = ((a ← (x=0 → y=0) →'
((b ← (x=0 → y=1) →'
((c ← y=0) →’
(d ← x=1)))) )⟩
z(3 0) // ev. c
z(1 3) // ev. d
z(3 3) // ev. θ (función no definida para los argumentos)
   
   
3. Función f de dos argumentos (x, y) que produce una secuencia de dos variables (u, v) con sus valores:
   
   

   x	y	u	v
   a	a	2	7
   b	a	3	4
   c	b	1	6
   d	b	5	9

   
   ⟨( f(x y) = ((x=a → y=a → ¡((u = 2) (v = 7)))
(x=b → y=a → ¡((u = 3) (v = 4)))
(x=c → y=b → ¡((u = 1) (v = 6)))
(x=d → y=b → ¡((u = 5) (v = 9))) )⟩

f(c b) // ev. (u=1 v=6)
f(0 0) // ev. θ (función no definida para los argumentos)

Funciones que devuelven funciones

Son funciones que retornan como resultado otra función. Ejemplos:

1. ⟨( f(n1 n2) = ⟨( g(n) = (n1 n2 … n) )⟩ )⟩
f(3 7) // ev. ⟨( g(n) = (3 7 … n) )⟩
   
   
2. ⟨( f(n1 n2) = ( ⟨( g(n) = (n1−n2 … n) )⟩ )⟩ ← n1>n2 →'
⟨( g(n) = (n1+n2 … n) )⟩ ) )⟩
f(3 7) // ev. ⟨( g(n) = (10 … n) )⟩
f(7 3) // ev. ⟨( g(n) = (4 … n) )⟩

Funciones como argumentos de funciones

Una función se pueden pasar como argumento de otra función. Ejemplo:

⟨( f(g n1 n2) = ⟨( ( [g([(n1…n2)!])] )/g ) )⟩ )⟩
f(⟨( g(n) = 2*n+1 )⟩ 1 4)
// ev. (g(1) g(2) g(3) g(4))/ ⟨( g(n) = 2*n+1 )⟩
// ev. (3 5 7 9)


Funciones de orden superior

Son funciones que tienen como funciones como argumentos y que retornan como resultado otra función. En general, una expresión paramétrica se puede pasar como argumento de una función. Ejemplos:

1. ⟨( f(u v) = ⟨( h(x y) = (u + v + 7) )⟩ )⟩
f(x*x y*y) // ev. ⟨( h(x y) = (x*x + y*y + 7) )⟩
   
   
2. ⟨( f(g n) = ⟨( h(x) = (n★g(x))/g )⟩ )⟩
f(⟨( g(x) = 2*x+1 )⟩ 4)
// ev. (⟨( h(x) = (4★g(x))/⟨( g(x) = 2*x+1 )⟩ )⟩ )⟩
// ev. (⟨( h(x) = (4★(2*x+1) )⟩

Aplicación de una función a una secuencia de argumentos

En MENTAL es fácil realizarlo mediante la primitiva “Distribución”.

Ejemplo con un parámetro:

⟨( triple(x) = 3×x )⟩
( [triple([1 2 3 4])] ) // ev. ( 3 6 9 12 )
( [triple[( 2…5 )])] ) // ev. ( 6 9 12 15 )

Ejemplo con dos parámetros:

⟨( f(x y) = (x+y x*y) )⟩
( [f[(1 2) (3 4) (5 6)]] ) // eq. ( f(1 2) f(3 4) f(5 6) )
// ev. ( (3 2) (7 12) (11 30) )

También se puede hacer mediante sustitución relativa. Para los dos ejemplos anteriores:

(1 2 3 4)/⟨( triple(n) = 3*n )⟩ // ev. ( 3 6 9 12 )

((1 2) (3 4) (5 6))/⟨( f(n1 n2) = (n1+n2 n1*n2) )⟩ // ev. ( (3 2) (7 12) (11 30) )

Obsérvese que los parámetros de la función tienen que indicar el tipo de elementos a los que se aplican (números enteros, en este caso).


Aplicación recursiva de una función

La aplicación recursiva (n veces) de una función f(x), con argumento a, es decir, por ejemplo, con n=4: f(f(f(f(a)))) se puede especificar mediante (f★n a)Δ siendo Δ el operador de agrupación binaria jerárquica, en este caso a la derecha. Recordemos que, por ejemplo,

(f f f a)Δ = f(f(f a))

Si el nombre de la función es fijo y el argumento a también, se podría definir la función de un parámetro:

⟨( z(n) = (f★n a)Δ )⟩

Ejemplo:

⟨( f(x y) = (x+y x*y) )⟩
⟨( z(n) = (f★n (a b))Δ )⟩
z(1) // ev. (f (a b)) eq. f(a b) ev. (a+b a*b)
z(2) // ev. (f (f (a b))) eq. f(f(a b)) // ev. ((a+b)+(a*b) (a+b)*(a*b))

Si el argumento x fuera variable, también podríamos definir la función de dos parámetros:

⟨( z(x n) = (f★n x)Δ )⟩

Ejemplo:

⟨( f(x y) = (x+y x*y) )⟩
z((a b) 1) // ev. (f (a b)) eq. f(a b) ev. (a+b a*b)
z((a b) 2) // ev. (f (f (a b))) eq. f(f(a b)) // ev. ((a+b)+(a*b) (a+b)*(a*b))

La máxima generalidad se logra cuando la propia función es también un parámetro:

⟨( z(f x n) = ((f★n x)Δ)/f )⟩

Ejemplo:

z(⟨( f(x y) = (x+y x*y) )⟩ (a b) 1) // ev. (f (a b))/⟨( f(x y) = (x+y x*y) )⟩ ev. (a+b a*b)

z(⟨( f(x y) = (x+y x*y) )⟩ (a b) 2) // ev. (f (f (a b)))/⟨( f(x y) = (x+y x*y) )⟩ ev. f(f(a b)) ev. ((a+b)+(a*b) (a+b)*(a*b))


Evaluación parcial de funciones

Se trata de suministrar menos argumentos que parámetros tiene definidos la función. Esto permite definir funciones particulares, instanciadas a partir de funciones más generales. Ejemplo:

⟨( f(x y) = (x+y x*y) )⟩
f(5 y) // ev. (5+y 5*y)
⟨( g(y) = f(5 y) )⟩ // ev. ⟨( g(y) = (5+y 5*y) )⟩
g(7) // ev. (12 35)

En MENTAL, el mecanismo de evaluación parcial es genérico, es decir, es aplicable a todo tipo de expresiones [ver Lenguaje MENTAL – Técnicas – Evaluación parcial].

---

Bibliografía

• Backus, John. Can Programming be liberated from the Von Neumann stile? A functional style and its algebra of programs. CACM, vol. 21, pp. 613-641, Ag. 1978.
  
  
• Cousineau, Guy; Mauny, Michel. The Functional Approach to Programming. Cambridge University Press
  
  
• Hudak, P. Conception, evolution and application of functional programming languages. ACM Computing Surveys, 21 (3), pp. 359-411, Sep. 1989.
  
  
• Jones, S.L. Peyton. The implementation of functional programming. Prentice-Hall, Englewood Cliffs, NJ, 1987.
  
  
• MacLennan, Bruce J. Functional Programming: Practice and Theory. Addison-Wesley Professional, 1990.
  
  
• Michaelson, Greg. An introduction to Functional Programming Through Lambda Calculus. Dover, 2011.
  
  
• Milewski, Jaroslaw. Functional Data Structures as Updatable Objects. IEEE Transactions on Software Engineering, vol. 16, no. 12, pp. 1427-1432, Dec. 1990.
  
  
• Turner, J.A. An overview of Miranda. ACM SIGPLAN Notices, 21 (12), pp. 158-166, Dic 1986.